Formule matematiche utili all'astrofilo
Di seguito una serie di formule molto utili per l'astrofografia, che il buon Giancarlo Calzetta si è preso la briga di chiedere in prestito dal sito di
Wilmslow Astro e di tradurre in italiano. Ringraziandolo per il permesso accordatomi, condivido anche io questo utile lavoro, approfittando
dell'occasione per arricchirlo ulteriormente con formule inserite da me.
Prego chiunque abbia suggerimenti o correzioni di segnalarmeli!
Ingrandimento visuale
Campo apparente e campo inquadrato reale degli oculari
Campo inquadrato dal CCD
Rapporto arcsec/pixel partendo dalla dimensione nota di un oggetto
Rapporto focale (F/) conoscendo il rapporto arcsec/pixel
Lunghezza focale partendo dalla dimensione nota di un oggetto
Dimensione di un oggetto sul sensore partendo da dimensione angolare e focale
Campionamento ideale CCD
Riduttori di focale
Proiezione da oculare
Ombre causate da polvere sul ccd
Riflessi dei filtri sul ccd
Magnitudine limite nel visuale
Rapporto segnale rumore
Dimensione disco di Airy
Errore periodico della montatura
Lunghezza della traccia delle stelle
Velocità autoguida
Zona critica per il fuoco & zona di fuoco CCD
Massima distanza filtro-sensore per evitare la vignettatura
Calcolatore entità della rotazione di campo
Torna all'indice
Ingrandimento visuale
L'ingrandimento di un telescopio in visuale è definito come rapporto fra lunghezza la focale dell'obiettivo e quella dell'oculare. Ciò però non significa che l'angolo sotto il quale osserviamo l'oggetto viene semplicemente moltiplicato per l'ingrandimento (per esempio la Luna, che sottende ad occhio nudo 30', a 400x sottenderebbe più di 180 gradi, che non ha senso). In realtà, per conoscere la dimensione angolare apparente dell'oggetto osservato bisogna invece applicare la formula che segue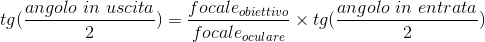
Campo apparente dell'oculare e corrispondente campo reale
Di seguito riportiamo due metodi: il primo è più approssimativo, ma più semplice da applicare dato che spesso non si conoscono le caratteristiche del field stop.Metodo 1
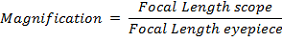
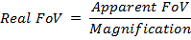
Metodo 2
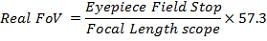
Torna all'indice
Campo inquadrato dal CCD in primi d'arco (ArcMin)
A partire dalla dimensione del CCD in millimetri o da risoluzione e dimensione pixel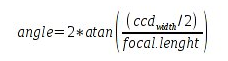
Metodo 1
Metodo 2
Torna all'indice
Rapporto arcsec/pixel partendo dalla dimensione nota di un oggetto
In alternativa, possiamo prendere la dimensione in arcosecondi di un oggetto e dividerla per le dimensioni dell'oggetto in pixel.
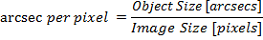
Torna all'indice
Rapporto focale (F/) conoscendo il rapporto arcsec/pixel
Conoscendo il rapporto arcsec/pixel, l'apertura e la dimensione del pixel, il rapporto focale si ricava come:
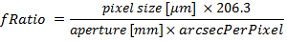
Torna all'indice
Lunghezza focale partendo dalla dimensione nota di un oggetto
Possiamo usare questa formula per ottenere una misurazione ragionevolmente accurata della lunghezza focale quando conosciamo le dimensioni apparenti in arcosecondi di un oggetto o la distanza, sempre apparente e in arcosecondi, tra due stelle e i corrispondenti valori in pixel:
![focal length = (object[pix] * pix_size * 206.3) / object[arcsec]](immagini/formule/formula28.png)
Torna all'indice
Dimensione di un oggetto sul sensore partendo da dimensione angolare e focale
Con questa formula è possibile calcolare la dimensione di un oggetto sul sensore CCD in mm e in pixel conoscendone la dimensione angolare in primi o secondi d'arco e sapendo la focale di ripresa.
![object[pix]=(focal length * object[arcsec])/(pix_size * 206.3)](immagini/formule/formula31.png)
Torna all'indice
Campionamento ideale nella ripresa CCD di pianeti
Questa formula ci fornisce la lunghezza focale minima necessaria per ottenere il massimo campionamento con una data CCD. La formula parte dal presupposto che il seeing e l'ottica siano perfetti. Utilizzando la tipica tecnica del "lucky imaging" con esposizioni brevi e tanti frame ripresi, l'assunto è ragionevole anche se non pienamente verificato. Un campionamento ideale, secondo questa formula, corrisponde alla risoluzione massima del telescopio spalmata su 3 pixel.
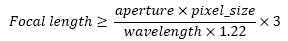
Torna all'indice
Riduttori di focale
Questa formula calcola la focale risultante quando si usa un riduttore di focale: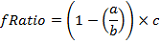
E questa calcola la quantità di backfocus che viene utilizzata dal riduttore su di un determinato setup:
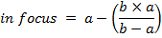
Dove:
a = Distanza del CCD dal riduttore di focale
b = lunghezza focale del riduttore
c = Rapporto focale del telescopio. I riduttori Celestron/Meade hanno le seguenti lunghezze focali.
[nota: intorno al 2006, Meade ha messo in circolazione dei riduttori 0.63 che avevano una lunghezza focale pari alla metà di quella che sarebbe dovuta essere, rendendoli inadatti all'uso con ruote portafiltri e Reflex. Quelli marchiati "Japan" sono OK così come lo sono quelli marchiati "China".]:FR 0.33x Lunghezza focale = 85mmWilliam Optics 0.8x FR Lunghezza focale = 260mm
FR 0.63x Lunghezza focale = 285mm
ATIK 0.5x FR Lunghezza focale = 80mm
* Notare che il calcolo del fuoco interno necessario presuppone che la necessaria distanza tra riduttore e CCD sia aggiunta al treno ottico, come quando si usano i raccordi Celestron o Meade per SC. Se si usa un riduttore di focale come quello Atik, che si inserisce all'interno del treno ottico già presente, allora si deve aggiungere la distanza al risultato (in modo da ridurlo). Se invece si usa un riduttore di focale come quello Meade/Celestron, allora bisogna sottrarre la lunghezza focale al risultato, per aumentarlo o renderlo negativo).
Torna all'indice
Proiezione da oculare
Questa formula serve per calcolare la focale (e il rapporto focale) risultante utilizzando la tecnica della proiezione da oculare: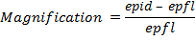
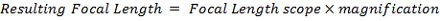
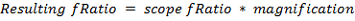
Dove:Note: Questa formula fornisce un valore approssimativo del rapporto focale e della lunghezza focale equivalente. La distanza dal CCD all'oculare è infatti difficile da misurare e il suo punto nodale (cioè il punto d'efficacia dell'oculare, che di solito si trova all'interno dell'oculare) è spesso sconosciuto.
epid = Distanza dell'oculare dal CCD
epfl = Lunghezza focale dell'oculare
Torna all'indice
Ombre causate da polvere lungo il percorso ottico
In caso di macchie sull'immagine del CCD dovute a granelli di polvere lungo il percorso ottico, può essere utile capire a che distanza si trova il granello dal sensore per poterlo eliminare. Questa formula consente di calcolare tale distanza: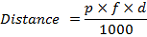
Dove:
Dist = Distanza in mm dalla superfice del CCD
p = Dimensione in micron dei pixel del CCD
f = Rapporto focale del sistema di ripresa
d = Diametro delle macchie di polvere in pixel
Torna all'indice
Riflessi dei filtri sul ccd
In caso di aloni attorno alle stelle, ecco una formula che ci dice quanto è distante dal ccd la loro fonte.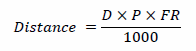
Dove:
Dist = Distanza dal CCD in mm
D = Diametro dei riflessi in pixel
P = Dimensione pixel CCD in micron
FR = Rapporto Focale del sistema di ripresa
Torna all'indice
Magnitudine limite visuale
Una formula approssimativa per calcolare la magnitudine limite in visuale per un dato telescopio è:
![VLM = 7.5 + (5 * Log(Aperture [cm]))](immagini/formule/formula15.png)
La magnitudine limite fotografica è di circa un paio di punti più debole.
Torna all'indice
Rapporto Segnale/Rumore
Questa è una formula semplificata per il calcolo del rapporto Segnale/Rumore:
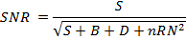
Dove:
S = Segnale complessivo del soggetto
B = Segnale complessivo del fondo
D = Corrente di dark
RN = Rumore di lettura del Bias
n = Numero delle pose
Torna all'indice
Diametro del disco di Airy
Questa è una formula per calcolare le dimensioni del disco di Airy prodotto da un telescopio:
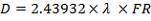
e
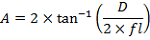
D = Diametro del disco di Airy in mm
λ = Lunghezza d'onda della luce in nm
FR = Rapporto focale del sistema di ripresa
A = Diametro angolare del disco di Airy
fl = Lunghezza focale del telescopio
Torna all'indice
Calcolo dell'errore periodico della montatura
Per calcolare l'errore periodico della montatura utilizzando un CCD o una webcam di solito si mettono in un foglio di calcolo una serie di dati che rappresentano lo scostamento di una stella ripresa e poi si crea un grafico. I dati rappresentano uno scostamento e un orario. Per convertire i valori dell'errore in arcosecondi, bisogna conoscere il rapporto arcosec/pixel della ripresa e la declinazione della stella. La formula completa è la seguente:
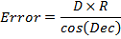
D = Deviazione della posizione della stella da quella inizialeNaturalmente si può eliminare la necessità di conoscere la declinazione della stella puntandone una in prossimità dell'equatore celeste..
R = Risoluzione della CCD in arcosecondi
Dec = Declinazione della stella
Torna all'indice
Lunghezza delle strisciate delle stelle
La seguente formula calcola la lunghezza delle tracce lasciate dalle stelle in una ripresa del cielo a camera fissa:
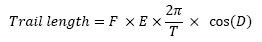
F = Lunghezza focale del telescopio (la lunghezza delle strisciate sarà espressa nella stessa unità di misura usata per questo dato)Oppure, per chi fa immagini CCD:
E = Durata delle esposizioni
T = Lunghezza del giorno siderale espressa nella stessa unità di misura della lunghezza delle esposizioni
D = Declinazione della stella
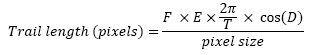
Torna all'indice
Velocità autoguida
Questa formula calcola di quanti pixel per secondo si muovere la montatura durante l'autoguida. Il calcolo parte dal presupposto che gli assi di ar e dec siano perfettamente allineati agli assi del sensore.
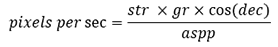
Dove:
str = Velocità di inseguimento siderale (15.04 arcsecs/secondo)
gr = Velocità di guida della montatura (frazione di quella siderale)
aspp = Rapporto arcsec/pixel della camera di guida o di ripresa
dec = Declinazione della stella
Torna all'indice
Zona critica del fuoco
La formula seguente calcola la lunghezza della zona in cui l'immagine di una stella a fuoco è più piccola del suo disco di Airy.
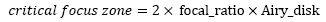
che può essere espressa come:
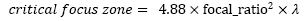
Per le camere CCD usiamo un campionamento a 2X:
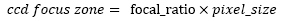
Dove:Nota: La zona critica del fuoco per i CCD è diversa perché con rapporti focali bassi la dimensione del disco di Airy diventa molto più piccola della dimensione media dei pixel delle CCD. Il valore della zona critica per il CCD, nel caso in cui il disco di Airy sia la metà della dimensione efficace dei pixel, assume quindi il valore "CCD focus zone" definito nella formula in alto, che fornisce un'indicazione più precisa della CFZ per gli astrofotografi.
λ = lunghezza d'onda della luce
Nota2: Se si utilizza una barlow o la proiezione dell'oculare, la zona critica del fuoco sul CCD sarà quella relativa al rapporto focale equivalente ottenuto, mentre la zona critica del fuoco in corrispondenza del focheggiatore resterà quella originale. In pratica, solo se il focheggiatore fosse montato a valle di una barlow nx, si avrebbe una profodità di fuoco aumentata di n^2 volte; per un focheggiatore posto a monte continua invece a valere la zona critica originaria propria del telescopio.
Torna all'indice
Massima distanza filtro-sensore per evitare la vignettatura
Questa formula calcola la massima distanza che può intercorrere fra il sensore e un filtro prima che compaiano effetti di vignettatura: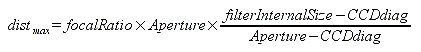
Torna all'indice
Rotazione di campo
A causa della rotazione terrestre, le foto astronomiche fatte ad esempio da un cavalletto sono naturalmente affette da rotazione di campo. L'uso di una montatura equatoriale ben stazionata o di un derotatore sono metodi comuni per eliminare il problema compensando tale effetto. Le foto fatte da una montatura equatoriale non correttamente stazionata rimangono invece affette da rotazione di campo. Questo anche se viene impiegata l'autoguida, che compensa le derive causate dal cattivo stazionamento ma non la rotazione. È quindi interessante conoscere la relazione fra errore di stazionamento e rotazione di campo per verificare in quali condizioni si verifica una rotazione non accettabile, cioè che genera evidente mosso. Un caso estremo in cui conoscere l'entità della rotazione di campo può essere interessante è l'astrofotografia planetaria fatta con montature altazimutali. In questo caso, anche se i singoli video sono troppo brevi per evidenziare l'effetto della rotazione di campo, per sommare frame presi a distanza di minuti è generalmente necessario ruotare opportunamente i frame per compensare il fenomeno. In pratica, la rotazione di campo appare avvenire attorno alla stella guida (o nel punto di riferimento scelto per l'allineamento fra più frame, in caso di somma di pose brevi non guidate). Ovviamente, i punti più lontani dal centro di rotazione mostreranno una sbavatura più evidente. La distanza dal centro di rotazione, così come lo spostamento delle stelle nel tempo, può essere misurata in primi d'arco, in mm o in pixel. A seconda dell'unità di misura scelta, può essere necessario conoscere anche la focale di ripresa per scalare correttamente il risultato, ma in generale la rotazione di campo, essendo un angolo, non dipende dalla focale di ripresa. La formula di seguito riportata usa il pixel come unità di misura, ed è quindi necessario conoscere la distanza in pixel fra il centro di rotazione e il punto in cui si osserva la rotazione. Ad esempio, se la stella guida si trova al centro del campo inquadrato, il primo valore da inserire è la metà della diagonale del sensore, che è poi lo stesso numero da usare nel caso in cui allineiamo a posteriori più frames ripresi in tempi diversi sul centro dell'immagine stessa. In output, un risultato in pixel maggiore di 1 indica che si avrà del mosso dovuto a rotazione di campo. La formula è approssimata per eccesso e si riferisce alla ripresa di un oggetto posto sul meridiano locale con errore in altezza (caso peggiore). La formula applicata è la seguente:![rotaz_in_pixel = dist_in_pixel*delta_t*(2 Pi Sin[error])/(T Sqrt[1 - (Cos[Dec] Sin[error] + Cos[error] Sin[Dec])^2])](immagini/formule/formula32.png)





![Validate my RSS feed [Valid RSS]](immagini/valid-rss-rogers.png)

